LeetCode 刷题预备知识

时间复杂度 & 空间复杂度

时间复杂度

最差情况的时间复杂度 & 空间复杂度（大 O 符号）。复杂度由低到高分别是：O(1)、O(log n)、O(n)、O(n log n)、O(n²)、O(n³)、O(2ⁿ)，O(n!)…

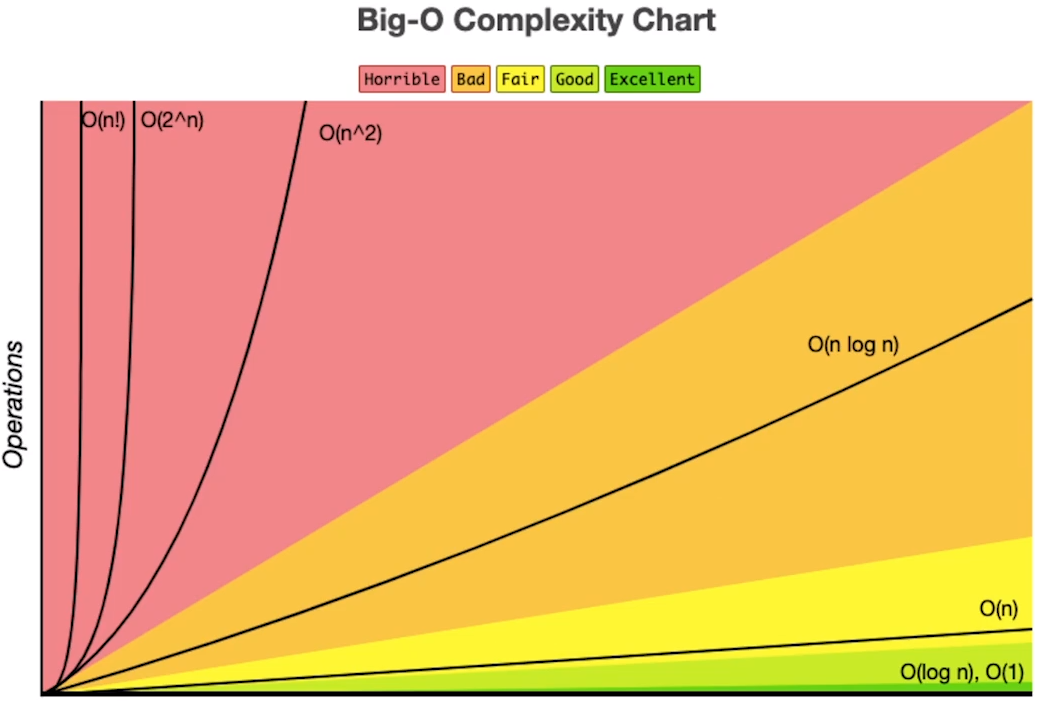
Big-O Complexity Chart

做题过程中通常关注到 O( n² )就可以了，后面复杂度过高，是需要被优化的情况。

时间复杂度为 O(1) 的例子：if(i == 1)、a = 1、result = 3 + 4、result = n * 2、result = 10000 * 10000、array.push(‘a’)、array.pop()、map.set(1, 1)、map.get(1)，
在计算复杂度的时候，O(1) 一般会被忽略，但也有时间复杂度为 O(1) 的题。

因为计算复杂度时，取复杂度最高的一项作为总体复杂度，前面的常数忽略。
比如：n3 + n2 + 1 的时间复杂度为 n3;
2n2 + 3n + 6 的时间复杂度为 n2;

时间复杂度为 O(n) 的例子：for 循环、while 循环 (不使用二分搜索)。

时间复杂度为 O(n²) 的例子：嵌套 for 循环、嵌套 while 循环。

for(let i = 0;i < n;i++){
    for(let j = 0;j < n;j++){
        a += i;
    }
}

下面的循环是两个循环分摊的一个循环工作，外层循环结束之后赋值 i 给 j，内部循环接着 i 开始的，所以时间复杂度还是 O(n)

while(i < n){
    i++; j = i;
    while(j < n){
        i++;
    }
}

空间复杂度

声明单一的变量就是空间复杂度为 O(1) 的例子: const a = 1; int a = ‘a’。

与时间复杂度不同，有很多题的空间复杂度都是 O(1)

空间复杂度为 O(n) 的例子：定义一个长度为 n 的数组；定义一个长度为 n 的 Set、Map；用 for 循环生成一个长度为 n 的链表。
空间复杂度为 O(n²) 的例子：二维数组，一维数组每个元素存放一个长度为 n 的 Set 或 Map 或链表。

复杂度优化

比较两个题解的优劣，涉及时间与空间复杂度时，一般考虑时间复杂度较低的那个，一个程序更快比较重要，若无特殊要求的话。
时间复杂度相同，就选择空间复杂度较低。

特别注意

Log n 一般是指二分搜索；N log n 是排序，array.sort()。

优化方法:
从低一级的复杂度寻找灵感
O(n) -> O(logn) 使用二分搜索；
O(nlogn) -> O(n) 遇到需要排序的题，考虑能否通过数组、Set、Map、Heap 解；
O(n²) -> O(nlogn) 遇到嵌套循环，考虑一下能否通过排序 + 一个 for 循环解。
https://leetcode-cn.com/problems/valid-anagram/
https://leetcode-cn.com/problems/merge-intervals

链表

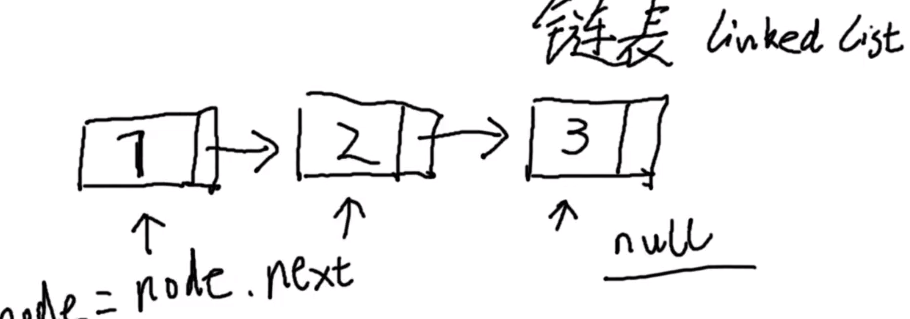
不停的 next 就可以一个个取到后面的值，最后一个 next 时得到 null。
链表添加和删除值比较方便，但是访问值时需要 O(n) 时间。因为链表里没有数组中直接通过下标取某个值的方法。
上面是单向链表，还有如下双向链表。

循环链表：

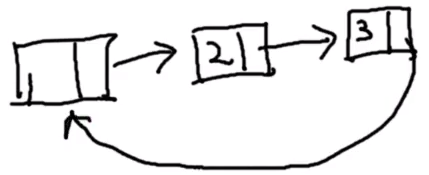
链表有环，这个环不一定指向链表最开始，也可能指向中间某个地方。

二叉树

来源：https://www.jianshu.com/p/bf73c8d50dc2
结点是数据结构中的基础，是构成复杂数据结构的基本组成单位。
树（Tree）是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：
1）有且仅有一个特定的称为根（Root）的结点；
2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、……、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。
此外，树的定义还需要强调以下两点：
1）n>0时根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。
2）m>0时，子树的个数没有限制，但它们一定是互不相交的。
结点拥有的子树数目称为结点的度。

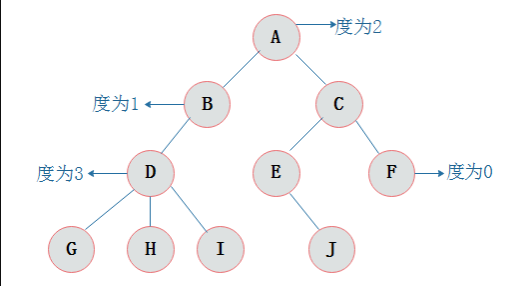
从根开始定义起，根为第一层，根的孩子为第二层，以此类推。最后没有节点的那些节点称为叶子。
树中结点的最大层次数称为树的深度或高度。下图所示树的深度为 4。

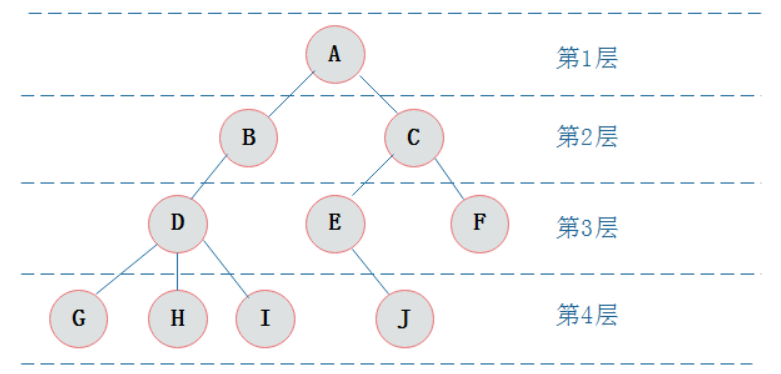
二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

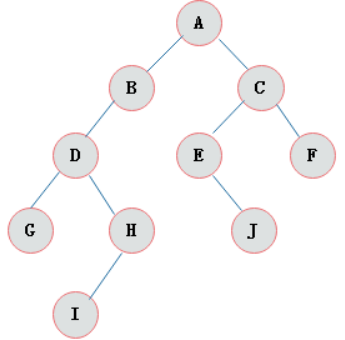
由二叉树定义以及图示分析得出二叉树有以下特点：
1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
二叉树性质：
1）在二叉树的第i层上最多有2i-1 个节点。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：

(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子，否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点，否则，编号为2i+1 的结点为其右孩子结点。

斜树：所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。
满二叉树 full binary tree：在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。
满二叉树的特点有：
1）叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
2）非叶子结点的度一定是2。
3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

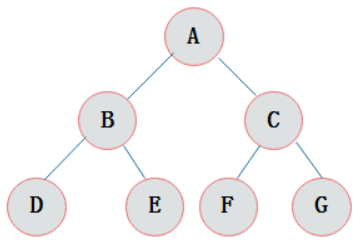
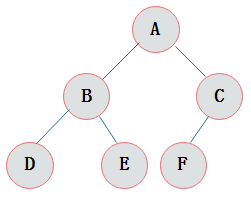
完全二叉树 complete binary tree：对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。
特点：
1）叶子结点只能出现在最下层和次下层。
2）最下层的叶子结点集中在树的左部。
3）倒数第二层若存在叶子结点，一定在右部连续位置。
4）如果结点度为1，则该结点只有左孩子，即没有右子树。
5）同样结点数目的二叉树，完全二叉树深度最小。
注：满二叉树一定是完全二叉树，但反过来不一定成立。

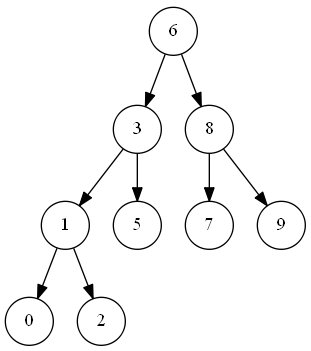
重点二叉搜索树 BST

二叉搜索树是一种节点值之间具有一定数量级次序的二叉树，对于树中每个节点：

若其左子树存在，则其左子树中每个节点的值都不大于该节点值；
若其右子树存在，则其右子树中每个节点的值都不小于该节点值。

BST 与递归是天然融合的关系。
下面做一个二分查找的例子 https://www.bilibili.com/video/BV14f4y1C7hg?p=5&spm_id_from=pageDriver ：
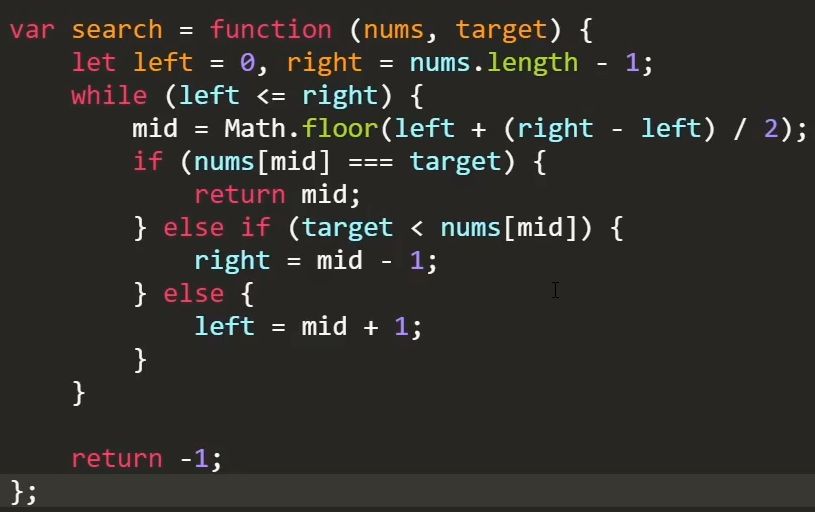
在一个排序过后的数组中找到目标值返回其 index，没找到返回 -1。
一般解题过程是遍历数组，找到值；二分查找是直接从数组中间开始查找，判断中间值与目标值大小，再决定向左还是向右继续查找，直到找到目标值。

Set 和 Map

Set

Set 对象是独一无二的值的集合。new 一个 Set ，然后可以用 add() 往里面放值，Set 特点：可以保证里面的元素都是不重复的。

往里面再加一个 1 ，Set 中仍然只有一个 1。
delete() 方法用来删除 Set 中的元素，如果所删除的值存在会删除成功并返回 true，若要删除的元素在 Set 中不存在则返回 false。
has() 方法判断 Set 有没有某一个元素。返回 true 或 false。
size() 方法判断 Set 的长度，有多少元素。
1
2
3
numberSet.forEach( number => {
console.log(number); // 遍历 Set 用 forEach()
})

Map

Map 与 Object 很像。

const myself = new Map(); // 往 Map 里添加东西用 set()
myself.set("name", "白醭飙尘");
myself.set("age", 23);
myself.set("hobby", ["前端", "读写", "足球"]); // value 可以是数组等

myself.get("name"); // get() 方法传入 key 获取值